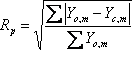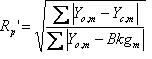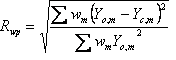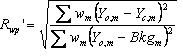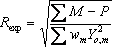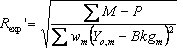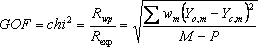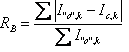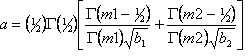Table of Contents
2 Introduction
This document describes the kernel operation of TOPAS together with its macro language. This includes the fully featured program TOPAS as well as its variants TOPAS R and TOPAS P.
This document describes the kernel operation of TOPAS-Academic together with its macro language. The kernel is written in ANSI c++. It’s internal data structures comprises a tree similar to an XML representation. Individual nodes of the tree corresponds to c++ objects. Understanding the internal tree structure facilitates successful operation.
Input is through an input file (*.INP) comprising readable “keywords” and “macros”, the latter being groupings of keywords. The INP file can be thought of as being an XML document but without the tags. INP format can be described by an XML schema but it is closer to a scripting/modeling language.
The kernel pre-processes the INP file expanding macros as required; the resulting pre-processed file (written to TOPAS.LOG) comprises keywords that are operated on by the kernel. On parsing the INP file the kernel creates the internal data structures. The main node objects are as follows :
top
xdd…
bkg ‘ Background
str… ‘ Structure information for Rietveld refinement
xo_Is… ‘ 2q - I values for single line or whole powder pattern fitting
d_Is… ‘ d - I values for single line or whole powder pattern fitting
hkl_Is… ‘ lattice information for Le Bail or Pawley fitting
fit_obj… ‘ User defined fit models
hkl_Is_from_hkl4 ‘ Structure factors (Fobs)2 for creating a powder pattern from single
‘ crystal data
str, xo_Is, d_Is and hkl_Is are referred to as “phases” and the peaks of these “phase peaks”. A full listing of the data structures are given in section 8.1.
2.1 Conventions
The following are used in this manual:
Ø Keywords are in italics.
Ø Keywords enclosed in square brackets [ ] are optional.
Ø Keywords ending in … indicate that multiple keywords of that type are allowed.
Ø Text beginning with the character # corresponds to a number.
Ø Text beginning with the character $ corresponds to a User defined string.
Ø E, !E or N placed after keywords have the following meaning:
E: An equation (ie. = a+b;) or constant (ie. 1.245) or a parameter name with a value (ie. lp 5.4013) that can be refined
!E: An equation or constant or a parameter name with a value that cannot be refined.
N: Corresponds to a parameter name.
To avoid input errors it is useful to differentiate between keywords, macros, parameter names, and reserved parameter names. The conventions followed so far are as follows:
Keywords : all lower case
Parameter names : first letter in lower case
Macro names : first letter in upper case
Reserved parameter names : : first letter in upper case
2.2 Input file example (INP format)
The following is an example input file for Rietveld refinement of a phase mixture of corundum and fluorite:
/*
Rietveld refinement comprising two phases.
*/
xdd filename
CuKa5(0.001)
Radius(217.5)
LP_Factor(26.4)
Full_Axial_Model(12, 15, 12, 2.3, 2.3)
Slit_Width(0.1)
Divergence(1)
ZE(@, 0)
bkg @ 0 0 0 0 0 0
STR(R-3C, “Corundum Al2O3”)
Trigonal(@ 4.759, @ 12.992)
site Al x 0 y 0 z @ 0.3521 occ Al+3 1 beq @ 0.3
site O x @ 0.3062 y 0 z 0.25 occ O-2 1 beq @ 0.3
scale @ 0.001
CS_L(@, 100)
r_bragg 0
STR(Fm-3m, Fluorite)
Cubic(@ 5.464)
site Ca x 0 y 0 z 0 occ Ca 1 beq @ 0.5
site F x 0.25 y 0.25 z 0.25 occ F 1 beq @ 0.5
scale @ 0.001
CS_L(@, 100)
r_bragg 0
The format is case sensitive. Optional indentation can be used to show tree dependencies. Within a particular tree level placement is not important. For example, the keyword str signifies that all information (pertaining to str) occurring between this keyword and the next one of the same level (in this case str) applies to the first str.
All input text streams can have line and/or block comments. A line comment is indicated by the character ' and a block comment by an opening /* and closing */. Text from the line comment character to the end of the line is ignored. Text within block comments are also ignored; block comments can be nested. Here are some examples:
' This is a line comment
space_group C_2/c ' Text to the end of this line is ignored
/*
This is a block comment.
A block comment can consist of any number of lines.
*/
On termination of refinement an output parameter file (*.OUT) similar to the input file is created with refined values updated.
The variants TOPAS P and TOPAS R support the fit objects as indicated in Table 2‑1. Descriptions of unsupported fit objects and their dependents in this manual may be ignored by the user.
Table 2‑1: Fit objects supported by TOPAS and its variants.
| Fit Objects | TOPAS | TOPAS R | TOPAS P |
| xo_Is, d_Is | ü | û | ü |
| hkl_Is | ü | ü | ü |
| str | ü | ü | û |
2.3 Test examples
The directory TEST_EXAMPLES contains many examples that can act as templates for creating INP files. In addition there are charge-flipping examples found in the CF directory and indexing examples in the INDEXING directory.
3 Parameters
3.1 When is a parameter refined
A parameter is flagged for refinement by giving it a name. The first character of the name can be an upper or lower case letter; subsequent characters can additionally include the underscore character '_' and the numbers 0 through 9. For example:
site Zr x 0 y 0 z 0 occ Zr+4 1 beq b1 0.5
Here b1 is a name given to the beq parameter. No restrictions are placed on the length of parameter names. The character ! placed before b1, as in !b1, signals that b1 is not to be refined, for example:
site Zr x 0 y 0 z 0 occ Zr+4 1 beq !b1 0.5
A parameter can also be flagged for refinement using the character @; internally the parameter is given a unique name and treated as an independent parameter. For example:
site Zr x 0 y 0 z 0 occ Zr+4 1 beq @ 0.5
or, site Zr x 0 y 0 z 0 occ Zr+4 1 beq @b1 0.5
The b1 text is ignored in the case of @b1.
3.2 User defined parameters - the prm keyword
The [prm|local E] keyword defines a new parameter. For example:
prm b1 0.2 ' b1 is the name given to this parameter
' 0.2 is the initial value
site Zr x 0 y 0 z 0 occ Zr+4 0.5 beq = 0.5 + b1;
occ Ti+4 0.5 beq = 0.3 + b1;
Here b1 is a new parameter that will be refined; this particular example demonstrates adding a constant to a set of beq's. Note the use of the '=' sign after the beq keyword indicating that the parameter is not in the form of N #value but rather an equation. In the following example b1 is used but not refined:
prm !b1 .2
site Zr x 0 y 0 z 0 occ Zr+4 0.5 beq = 0.5 + b1;
occ Ti+4 0.5 beq = 0.3 + b1;
Parameters can be assigned the following attribute equations that can be functions of other parameters:
[min !E] [max !E] [del !E] [update !E] [stop_when !E] [val_on_continue !E]
The min and max keywords can be used to limit parameter values, for example:
prm b1 0.2 min 0 max = 10;
Here b1 is constrained to within the range 0 to 10. min and max can be equations and thus they can be functions of other parameters. Limits are very effective in refinement stabilization.
del is used for calculating numerical derivatives with respect to the calculated pattern. This occurs when analytical derivatives are not possible.
update is used to update the parameter value at the end of each iteration; this defaults to the following:
new_Val = old_Val + Change
When update is defined then the following is used:
new_Val = “update equation”
The update equation can additionally be a function of the reserved parameter names Change and Val. The use of update does not negate min and max.
stop_when is a conditional statement used as a stopping criterion. In this case convergence is determined when stop_when evaluates to a non-zero value for all defined stop_when attributes for refined parameters and when the chi2_convergence_criteria condition has been met.
val_on_continue is evaluated when continue_after_convergence is defined. It supplies a means of changing the parameter value after the refinement has converged where:
new_Val = val_on_continue
Here are some example attribute equations as applied to the x parameter
x @ 0.1234
min = Val-.2;
max = Val+.2;
update = Val + Rand(0, 1) Change;
stop_when = Abs(Change) < 0.000001;
3.3 Parameter constraints
Equations can be a function of parameter names providing a mechanism for introducing linear and non-linear constraints, for example,
site Zr x 0 y 0 z 0 occ Zr+4 zr 1 beq 0.5
occ Ti+4 = 1-zr; beq 0.3
Here the parameter zr is used in the equation “= 1-zr;”. This particular equation defines the Ti+4 site occupancy parameter. Note, equations start with an equal sign and end in a semicolon.
min/max keywords can be used to limit parameter values. For example:
site Zr x 0 y 0 z 0
occ Zr+4 zr 1 min=0; max=1; beq 0.5
occ Ti+4 = 1-zr; beq 0.3
here zr will be constrained to within 0 and 1. min/max are equations themselves and thus they can a function of named parameters.
An example for constraining the lattice parameters a, b, c to the same value as required for a cubic lattice is as follows:
a lp 5.4031
b lp 5.4031
c lp 5.4031
Parameters with names that are the same must have the same value. An exception is thrown if the “lp” parameter values above were not all the same. Another means of constraining the three lattice parameters to the same value is by using equations with the parameter “lp” defined only once as follows:
a lp 5.4031
b = lp;
c = lp;
More general again is the use of the Get function as used in the Cubic macro as follows:
a @ 5.4031 b = Get(a); c = Get(a);
here the constraints are formulated without the need for a parameter name.
3.4 The local keyword
The local keyword is used for defining named parameters as local to the top level, xdd level or phase level. For example, the following code fragment:
xdd…
local a 1
xdd…
local a 2
actually has two 'a' parameters; one that is dependent on the first xdd and the other dependent on the second xdd. Internally two independent parameters are generated, one for each of the 'a' parameters; this is necessary as the parameters require separate positions in the A matrix for minimization, correlation matrix, errors etc…
In the code fragment:
local a 1 ‘ top level
xdd…
gauss_fwhm = a; ‘ 1st xdd
xdd…
local a 2 ‘ xdd level
gauss_fwhm = a; ‘ 2nd xdd
the 1st xdd will be convoluted with a Gaussian with a FWHM of 1 and the 2nd with a Gaussian with a FWHM of 2. In other words the 1st gauss_fwhm equation uses the ‘a’ parameter from the top level and the second gauss_fwhm equation uses the ‘a’ parameter defined in the 2nd xdd. This is analogous, for example, to the scoping rules found in the c programming language.
The following is not valid as b1 is defined twice but in a different manner.
xdd…
local a 1
prm b1 = a;
xdd
local a 2
prm b1 = a;
The following comprises 4 separate parameters and is valid:
xdd…
local a 1
local b1 = a;
xdd
local a 2
local b1 = a;
local can greatly simplify complex INP files.
3.5 Reporting on equation values
When an equation is used in place of a parameter 'name' and 'value' as in
occ Ti+4 = 1-zr;
then it is possible to obtain the value of the equation by placing “ : 0” after it as follows:
occ Ti+4 = 1-zr; : 0
After refinement the “0” is replaced by the value of the equation. The error associated with the equation is also reported when do_errors is defined.
3.6 Naming of equations
Equations can be given a parameter name, for example:
prm !a1 = a2 + a3/2; : 0
The a1 parameter here represents the equation “a2 + a3/2”. If the value of the equation evaluates to a constant then a1 would be an independent parameter, otherwise a1 is treated as a dependent parameter. If the equation evaluates to a constant then a1 will be refined depending on whether the ‘!’ character is placed before its name or not. After refinement the value and error associated with a1 is reported. This following equation is valid even though it does not have a parameter name; its value and error are also reported on termination of refinement.
prm = 2 a1^2 + 3; : 0
Equations are not evaluated sequentially, for example, the following:
prm a2 = 2 a1; : 0
prm a1 = 3;
gives on termination of refinement:
prm a2 = 2 a1; : 6
prm a1 = 3;
Non-sequential evaluation of equations are possible as parameters cannot be defined more than once with different values or equations; the following examples leads to redefinition errors:
prm a1 = 2; prm a1 = 3; ‘ redefinition error
prm b1 = 2 b3; prm b1 = b3; ‘ redefinition error
3.7 Parameter errors and correlation matrix
When do_errors is defined parameter errors and the correlation matrix are generated at the end of refinement. The errors are reported following the parameter value as follows:
a lp 5.4031_0.0012
Here the error in the lp parameter is 0.0012. The correlation matrix is identified by C_matrix_normalized and is appended to the OUT file if it does not already exist.
3.8 Default parameter limits and LIMIT_MIN / LIMIT_MAX
Parameters with internal default min/max attributes are shown in Table 3‑1. These limits avoid invalid numerical operations and equally important they stabilize refinement by directing the minimization routines towards lower ![]() values. Hard limits are avoided where possible and instead parameter values are allowed to move within a range for a particular refinement iteration. Without limits refinement often fails in reaching a low
values. Hard limits are avoided where possible and instead parameter values are allowed to move within a range for a particular refinement iteration. Without limits refinement often fails in reaching a low ![]() . User defined min/max limits overrides the defaults. min/max limits should be defined for parameters defined using the prm|local keyword.
. User defined min/max limits overrides the defaults. min/max limits should be defined for parameters defined using the prm|local keyword.
Functionality is often realized through the use of the standard macros as defined in TOPAS.INC; this is an important file to view. Almost all of the prm keywords defined within this file have associated limits. For example, the CS_L macro defines a crystallite size parameter with a min/max of 0.3 and 10000 nanometers respectively.
On termination of refinement, independent parameters that refined close to their limits are identified by the text “_LIMIT_MIN_#” or “_LIMIT_MAX_#” appended to the parameter value. The '#' corresponds to the limiting value. These warnings can be surpressed using the keyword no_LIMIT_warnings.
Table 3‑1 Default parameter limits.
| Parameter | min | max |
| la | 1e-5 | 2 Val + 0.1 |
| lo | Max(0.01, Val-0.01) | Min(100, Val+0.01) |
| lh, lg | 0.001 | 5 |
| a, b, c | Max(1.5, 0.995 Val - 0.05) | 1.005 Val + 0.05 |
| al, be, ga | Max(1.5, Val - 0.2) | Val + 0.2 |
| scale | 1e-11 | |
| sh_Cij_prm | -2 Abs(Val) - 0.1 | 2 Abs(Val) + 0.1 |
| occ | 0 | 2 Val + 1 |
| beq | Max(-10, Val-10) | Min(20, Val+10) |
| pv_fwhm, h1, h2, spv_h1, spv_h2 | 1e-6 | 2 Val + 20 Peak_Calculation_Step |
| pv_lor, spv_l1, spv_l2 | 0 | 1 |
| m1, m2 | 0.75 | 30 |
| d | 1e-6 | |
| xo | Max(X1, Val - 40 Peak_Calculation_Step) | Min(X2, Val + 40 Peak_Calculation_Step) |
| I | 1e-11 | |
| z_matrix radius | Max(0.5, Val .5) | 2 Val |
| z_matrix angles | Val – 90 | Val + 90 |
| rotate | Val – 180 | Val + 180 |
| x, ta, qa, ua | Val - 1/Get(a) | Val + 1/Get(a) |
| y, tb, qb,ub | Val - 1/Get(b) | Val + 1/Get(b) |
| z, tc, qc, uc | Val - 1/Get© | Val + 1/Get© |
| u11, u22, u33 | Val If(Val < 0, 2, 0.5) - 0.05 | Val If(Val < 0, 0.5, 2) + 0.05 |
| u12, u13, u23 | Val If(Val < 0, 2, 0.5) - 0.025 | Val If(Val < 0, 0.5, 2) + 0.025 |
| filament_length | 0.0001 | 2 Val + 1 |
| sample_length, receiving_slit_length, primary_soller_angle, secondary_soller_angle | ||
3.9 Reserved parameter names
Table 3‑2 and Table 3‑4 lists reserved parameter names that are interpreted internally. Table 3‑3 details dependices for certain reserved parameter names. An exception is thrown when a reserved parameter name is used for a User defined parameter name. An example use of reserved parameter names is as follows:
weighting = Abs(Yobs-Ycalc)/(Max(Yobs+Ycalc,1) Max(Yobs,1) Sin(X Deg/2));
Here the weighting keyword is written in terms of the reserved parameter names Yobs, Ycalc and X.
Table 3‑2 Reserved parameter names.
| Name | Description |
| A_star, B_star, C_star | Corresponds to the lengths of the reciprocal lattice vectors. |
| Change | Returns the change in a parameter at the end of a refinement iteration. Change can only appear in the equations update and stop_when. |
| D_spacing | Corresponds to the d-spacing of phase peaks in Å. |
| H, K, L, M | hkl and multiplicity of phase peaks. |
| Iter, Cycle, Cycle_Iter | Returns the current iteration, the current cycle and the current iteration within the current cycle respectively. Can be used in all equations. |
| Lam | Corresponds to the wavelength lo of the emission profile line with the largest la value. |
| Lpa, Lpb, Lpc | Corresponds to the a, b and c lattice parameters respectively. |
| Mi | An iterator used for multiplicities. See the PO macro of TOPAS.INC for an example of its use. |
| Peak_Calculation_Step | Return the calculation step for phase peaks, see x_calculation_step. |
| QR_Removed, QR_Num_Times_Consecutively_Small | Can be used in the quick_refine_remove equation. |
| R, Ri: | The distance between two sites R and an iterator Ri. Used in the equation part of atomic_interaction, box_interaction and grs_interaction. |
| Rp, Rs | Primary and secondary radius respectively of the diffractometer. |
| T | Corresponds to the current temperature, can be used in all equations.. |
| Th | Corresponds to the Bragg angle (in radians) of hkl peaks. |
| X, X1, X2 | Corresponds to the measured x-axis, the start and the end of the x-axis respectively. X is used in fit_obj's equations and the weighting equation. X1 and X2 can be used in all xdd dependent equation. |
| Xo | Corresponds to the current peak position; this corresponds to 2Th degrees for x-ray data. |
| Val | Returns the value of the corresponding parameter. |
| Yobs, Ycalc, SigmaYobs | Yobs and Ycalc correspond to the observed and calculated data respectively. SigmaYobs corresponds to the estimated standard deviation in Yobs.; can be used in the weighting equation. |
Table 3‑3 Parameters that operate on phase peaks. Note, dependencies are not shown.
| Keywords that can be a function of H, K, L M, Xo, Th and D_spacing. | ||
| lor_fwhm gauss_fwhm hat one_on_x_conv exp_conv_const circles_conv | stacked_hats_conv user_defined_convolution th2_offset scale_pks h1, h2, m1, m2 spv_h1, spv_h2, spv_l1, spv_l2 | pv_lor, pv_fwhm ymin_on_ymax la, lo, lh, lg phase_out scale_top_peak pk_xo |
Table 3‑4 Phase intensity reserved parameter names.
3.10 Val and Change reserved parameter names
Val is a reserved parameter name corresponding to the #value of a parameter during refinement. Change is a reserved parameter name which corresponds to the change in a refined parameter at the end of an iteration. It is determined as follows:
“Change” = “change as determined by non-linear least squares”
Val can only be used in the attribute equations min, max, del, update, stop_when and val_on_continue. Change can only be used in the attribute equations update and stop_when. Here are some examples:
min 0.0001
max = 100;
max = 2 Val + .1;
del = Val .1 + .1;
update = Val + Rand(0,1) Change;
stop_when = Abs(Change) < 0.000001;
val_on_continue = Val + Rand(-Pi, Pi);
x @ 0.1234 update=Val + 0.1 ArcTan(Change 10); min=Val-.2; max=Val+.2;
4 Equation Operators and Functions
Table 4‑1: Operators and functions supported in equations (case sensitive). In addition equations can be functions of User defined parameter names.
| Classes | Symbols / Functions | Remarks |
| Parentheses | () or [] | |
| Arithmetic | + | |
| - | ||
| * | The multiply sign is optional. (x*y = x y) | |
| / | ||
| ^ | x^y, Calculates x to the power of y. Precedence: x^y^z = (x^y)^z x^y*z = (x^y)*z x^y/z = (x^y)/z |
|
| Conditional | a == b | Returns 1 if a = b |
| a < b | Returns 1 if a < b | |
| a ⇐ b | Returns 1 if a ⇐ b | |
| a > b | Returns 1 if a > b | |
| a >= b | Returns 1 if a >= b | |
| And(a, b, …) | Returns 1 if all arguments evaluates to non-zero values. | |
| Or(a, b, …) | Returns true if one arguments evaluates to non-zero | |
| Mathematical | Sin(x) | Returns the sine of x |
| Cos(x) | Returns the cosine of x | |
| Tan(x) | Returns the tangent of x | |
| ArcSin(x) | Returns the arc sine of x (-1 ⇐ x ⇐ 1) | |
| ArcCos(x) | Returns the arc cos of x (-1 ⇐ x ⇐ 1) | |
| ArcTan(x) | Returns the arc tangent of x | |
| Exp(x) | Returns the exponential e to the x | |
| Ln(x) | Returns the natural logarithm of x | |
| Sqrt(x) | Returns the positive square root | |
| Special | Sum(returns summation_eqn, initializer, conditional_test, increment_eqn) | |
| If(conditional_test, return true_eqn, return false_eqn) | ||
| For(Mi = 0, Mi < M, Mi = Mi+1 ,….) | ||
| Get($keyword) | Gets the parameter associated with $keyword | |
| Miscellaneous | Min(a,b,c…) | Returns the min of all arguments |
| Max(a,b,c…) | Returns the max of all arguments | |
| Abs(x) | Returns the absolute value of x | |
| Mod(x, y) | Returns the modulus of x/y. Mod(x, 0) returns 0 | |
| Rand(x1, x2) | Returns a random number between x1 and x2 | |
| Sign(x) | Returns the sign of x, or zero if x = 0 | |
| Break | Can be used to terminate loops implied by the equations atomic_interaction, box_interaction and grs_interaction. | |
| Break_Cycle | Can be used to terminate a refinement cycle. For example, if a particular penalty is greater than a particular value then the refinement cycle can be terminated as follows: atomic_interaction ai = (R-1.3)^2; … penalty = If( ai > 5, Break_Cycle, 0); | |
In addition the following functions are implemented:
AB_Cyl_Corr(mR), AL_Cyl_Corr(mR):
Returns AB and AL for cylindrical sample intensity correction (Sabine et al., 1998). These functions are used in the macros Cylindrical_I_Correction and Cylindrical_2Th_Correction. Example CYLCORR.INP demonstrates the use of these macros. For a more accurate alternative to the Sabine corrections see the capillary_diameter_mm convolution.
Constant(expression)
Evaluates “expression” only once and then replaces Constant(expression) with the corresponding numeric value. Very useful when the expected change in a parameter insignificantly affects the value of a dependent equation, see for example the TOF macros such as TOF_Exponential.
Get_Prm_Error($prm_name)
Returns the error of the parameter $prm_name.
PV_Lor_from_GL(gauss_FWHM, lorentzian_FWHM):
Returns the Lorentzian contribution of a pseudo-Voigt approximation to the Voigt where gauss_FWHM, lorentzian_FWHM are the FWHMs of the Gaussian and Lorentzian convoluted to form the Voigt.
Voigt_Integral_Breadth_GL(gauss_FWHM, lorentzian_FWHM):
Returns the integral breadth resulting from the convolution of a Gaussian with a Lorentzian with FWHMs of gauss_FWHM and Lorentzian_FWHM respectively.
Voigt_FWHM_GL(gauss_FWHM, lorentzian_FWHM):
Returns the Voigt FWHM resulting from the convolution of a Gaussian with a Lorentzian with FWHMs of gauss_FWHM and Lorentzian_FWHM respectively.
Yobs_dx_at(#x)
Returns the step size in the observed data at the x-axis position #x; can be used in all sub xdd dependent equations. If the step size in the x-axis is equidistant then Yobs_dx_at is converted to a constant corresponding to the step size in the data.
4.1 'If' and nested 'if' statements
'Sum' and 'If' statements can be used in parameter equations, for example:
str…
prm a .1
prm b .1
lor_fwhm = If(Mod(H, 2)==0, a Tan(Th), b Tan(Th));
Min and Max can also be used in parameter equations; for example the following is valid:
prm a .1
th2_offset = Min(Max(a, -.2), .2);
'If' should be preferred in non-attribute equations as analytical derivatives are possible; they can be nested, for example:
prm cs 200 update =
If(Val < 10, 10,
If(Val > 10000, 10000,
Val
)
);
For those who are familiar with if/else statements then the IF THEN ELSE ENDIF macros as defined in TOPAS.INC can be used as follows:
IF a > b THEN
a ‘ return expression value
ELSE
b ‘ return expression value
ENDIF
4.2 Floating point exceptions
An exception is thrown when an invalid floating point operation is encountered, examples are:
Divide by zero.
Sqrt(x) for x < 0
Ln(x) for x ⇐ 0
ArcCos(x) for x < -1 or x > 1
Exp(x) produces an overflow for x ~> 700
(-x)^y for x > 0 and y not an integer
Tan(x) evaluates to Infinity for x = n Pi/2, Abs(n) = 1, 3, 5,…
min/max equations, or Min/Max functions or ‘If’ statements can be used to avoid invalid floating point operations. Equations can also be manipulated to yield valid floating point operations, for example, Exp(-1000) can be used in place of 1/Exp(1000).
5 The Minimization Routines
The Newton-Raphson non-linear least squares method is used by default with the Marquardt method (1963) included for stability. A Bound Constrained Conjugate Gradient (BCCG) method (Coelho, 2005) incorporating min/max limits is used for solving the normal equations. The objective function ![]() is written as:
is written as:
Yo,m and Yc,m are the observed and calculated data respectively at data point m, M the number of data points, wm the weighting given to data point m which for counting statistics is given by wm=1/s(Yo,m)2 where s(Yo,m) is the error in Yo,m, Pp are penalty functions, Np the number of penalty functions and K1 and K2,p are weights applied to the penalty functions and are described below. K normalizes ![]() such that the default chi2_convergence_criteria value of 0.001 is sufficient for routine refinements. Typical chi2_convergence_criteria values for structure determination range from 0.01 to 0.1. Penalty functions are minimized when there are no observed data Yo; see example onlypena.inp.
such that the default chi2_convergence_criteria value of 0.001 is sufficient for routine refinements. Typical chi2_convergence_criteria values for structure determination range from 0.01 to 0.1. Penalty functions are minimized when there are no observed data Yo; see example onlypena.inp.
The normal equations are generated by the usual expansion of Yc,m to a first order Taylor series around the parameter vector p ignoring second order terms. The size of p corresponds to the number of independent parameters N. The penalty functions are expanded to a second order Taylor series around the parameter vector p. The resulting normal equations are:
| A Dp = Y | (5‑4) |
| where A = A1 + A2 |
The Taylor coefficients Dp correspond to changes in the parameters p. Eq. (5‑4) represents a linear set of equations in Dp that are solved for each iteration of refinement. The calculation of the off diagonal terms in A2 (the second derivatives of the penalty functions) are tedious and preliminary investigations have indicated that their inclusion does not significantly improve convergence of![]() ; A2,ij for i¹j are therefore set to zero.
; A2,ij for i¹j are therefore set to zero.
The penalty weighting K2,i is used to give equal weights to the sum of the inverse error terms in the parameters s1(pi)2 and s2(pi)2 calculated from ![]() and
and ![]() respectively. Neglecting the off diagonal terms gives s1(pi)2=1/A1,ii and s2(pi)2=1/B2,ii and thus K2,i is written as shown in Eq. (5‑6).
respectively. Neglecting the off diagonal terms gives s1(pi)2=1/A1,ii and s2(pi)2=1/B2,ii and thus K2,i is written as shown in Eq. (5‑6).
The penalty weighting K1 determines the weight given to the penalties ![]() relative to
relative to ![]() , typical values range from 0.2 to 2.
, typical values range from 0.2 to 2.
5.1 The Marquardt method
The Marquardt (1963) method applies a scaling factor to the diagonal elements of the A matrix when the solution to the normal equations of Eq. (5‑4) fails to reduce![]() , or,
, or,
| Aii,scaled = Aii (1+h) |
where h is the Marquardt constant. After applying the Marquardt constant the normal equations are again solved and ![]() recalculated; this scaling process is repeated until
recalculated; this scaling process is repeated until ![]() reduces. Repeated failure results in a very large Marquardt constant and taken to the limit the off diagonal terms can be ignored and the solution to the normal equations can be approximated as:
reduces. Repeated failure results in a very large Marquardt constant and taken to the limit the off diagonal terms can be ignored and the solution to the normal equations can be approximated as:
| Dpi = Yi / (Aii (1 + h)) | (5‑7) |
The Marquardt method is used when the refinement comprises observed data Yo. The keyword no_normal_equations prevents the use of the Marquardt method.
The Marquardt constant h is automatically determined each iteration. Its determination is based on the actual change in ![]() and the expected change in
and the expected change in ![]() .
.
5.2 Approximating the A matrix - the BFGS method
The approximate_A keyword can be used to approximate the A matrix, Eq. (5‑4), without the need to calculate the A matrix dot products. The approximation is based on the BFGS method (Broyden, 1970; Fletcher, 1970; Goldfarb, 1970; Shanno, 1970). BCCG is used by default for solving the normal equations, alternatively, LU-decomposition can be used if use_LU is defined and the A matrix is not sparse. Note, that LU-decomposition requires the full A matrix and thus it may be too memory intensive for problems with 10s of thousands of parameters. LU-decomposition can also be too slow when the number of parameters is greater than about one thousand parameters.
Approximating A is useful when the calculation of the A matrix dot products is proving too expensive. When penalties dominates a refinement then the use of approximate_A may also improve convergence. approximate_A cannot be used with line_min or use_extrapolation.
The single crystal refinement examples AE14-APPROX-A.INP and AE1-APPROX-A.INP are cases where the use of approximate_A achieves convergence is less time than with the calculated A matrix.
When using approximate_A the A matrix can be made sparse by defining A_matrix_memory_allowed_in_Mbytes and/or A_matrix_elements_tollerance. This allows for the refinement of a very large number of parameters.
5.3 Line minimization and Parameter extrapolation
Line minimization better known as the steepest decent method is invoked with the keyword line_min. It uses a direction in parameter space given by Dpi=Yi/Aii to minimize on ![]() (p+lDp) by adjusting l.
(p+lDp) by adjusting l.
Parameter Extrapolation, invoked with the keyword use_extrapolation uses parabolic extrapolation of the parameters as a function of iteration, or, l is adjusted such that ![]() (al2+bl+c) is minimized where for a particular parameter pi at iteration k we have ai=(y1-2y2+y3)/2, bi=(y3-y1)/2 and ci=y2 where y1=(pi,k-5+pi,k-4)/2, y2=(pi,k-3+pi,k-2)/2 and y3 = (pi,k-1+pi,k-0)/2. Parameter Extrapolation encompasses the last six sets of parameter values. In cases where both
(al2+bl+c) is minimized where for a particular parameter pi at iteration k we have ai=(y1-2y2+y3)/2, bi=(y3-y1)/2 and ci=y2 where y1=(pi,k-5+pi,k-4)/2, y2=(pi,k-3+pi,k-2)/2 and y3 = (pi,k-1+pi,k-0)/2. Parameter Extrapolation encompasses the last six sets of parameter values. In cases where both ![]() and
and ![]() exists then Parameter Extrapolation reduces possible oscillatory behaviour in
exists then Parameter Extrapolation reduces possible oscillatory behaviour in ![]() . Parameter extrapolation when used with Line Minimization can increase the rate of convergence when refining on penalties only.
. Parameter extrapolation when used with Line Minimization can increase the rate of convergence when refining on penalties only.
Line minimization and Parameter Extrapolation have relatively small memory foot prints and thus can be useful when the A matrix consumes too much memory. Alternatively the approximate_A keyword can be used.
Line minimization with the full A matrix calculation (no approximate_A defined) can increase the rate of convergence on problems like Pawley refinement.
5.4 Minimizing on penalties only
When there are no observed data or when only_penalties is defined then by default the BFGS method is used, see examples rosenbrock-10.inp and HOCK.INP. For penalties only the BFGS method typically converges faster than line_min/use_extrapolation however for ‘penalties only’ it can be overridden with the use of line_min.
5.5 Summary, Iteration and Refinement Cycle
Table 5‑1 shows various keyword usages for typical refinement problems. The term “refinement cycle” is used to describe a single convergence. The reserved parameter Cycle returns the current refinement cycle with counting starting at zero. The reserved parameter Cycle_Iter returns the current iterations within a Cycle with counting starting at zero.
| Table 5‑1 Keyword sequences for various refinement types | ||
| Refinement type | Keywords to use | Comments |
| Rietveld refinement No penalties | Marquardt refinement. A matrix calculation. | |
| Rietveld refinement with a moderate number of penalties. | line_min (Maybe) | Line minimization used if line_min. Marquardt refinement. A matrix calculation. |
| Rietveld refinement dominated by penalties | approximate_A | BFGS method of refinement. A matrix approximation. |
| Pawley refinement | line_min | Line minimization. Marquardt refinement. A matrix calculation. |
| Penalties only | BFGS method of refinement. A matrix approximation. | |
| Refinements with a large number of parameters | approximate_A | BFGS method of refinement. A matrix approximation. |
5.6 quick_refine and computational issues
The computationally dominant factor of calculating Eq. (5‑5) is problem dependent. For Rietveld refinement with a moderate number of parameters then the calculation of the peak parameter derivatives may well be the most expensive. On the other hand for Rietveld refinement with a large number of structural parameters and data points then the calculation of the A1,ij dot products would be the dominant factor, where, the number of operations scale by M(N2+N)/2. Before the development of the BCCG routine (Coelho, 2005), the solution to the normal equations, Eq. (5‑4), was also very expensive.
For structure solution from powder data by simulated annealing, the keyword yobs_to_xo_posn_yobs can be used to reduce the number of data points M; thus reducing the number of operations in the A1,ij dot products, see the Decompose macro in example CIME-DECOMPOSE.INP.
The quick_refine keyword removes parameters during a refinement cycle thus shrinking the size of the A matrix by reducing N. Parameters are removed if the condition defined in Eq. (5‑8) is met for three consecutive iterations.
Alternatively, parameters can be removed or reinstated during a refinement cycle using quick_refine_remove. This keyword provides a means of performing block refining. If quick_refine_remove is not defined then all parameters are reinstated at the start of refinement cycles.
5.7 Auto_T and randomize_on_errors
It is sometimes difficult to formulate optimum val_on_continue functions for simulated annealing. This is especially true in structure solution using rigid bodies where optimum randomization of the rigid body parameters can be difficult to ascertain. randomize_on_errors is a means of automatically randomizing parameters based on the approximate errors in the parameters as given in Eq. (5‑9), where T is the current temperature and K is as defined in Eq. (5‑3).
Q is a scaling factor determined such that convergence to a previous parameter configuration occurs 7.5% of the time on average. When randomize_on_errors is used the magnitude of the temperature(s) is not of significance but the relative variation in temperature(s) are.
The macro Auto_T includes quick_refine, randomize_on_errors and a temperature regime. It has shown to be adequate for a wide range of simulated annealing examples, see example CIME-Z-AUTO.INP.
Note, when val_on_continue is defined then the corresponding parameter is not randomized according to randomize_on_errors.
5.8 Criteria of fit
Table 5‑2: Criteria of fit (see Young 1993 for details). Yo,m and Yc,m are the observed and calculated data respectively at data point m, Bkgm the background at data point m, M the number of data points, P the number of parameters, wm the weighting given to data point m which for counting statistics is given by wm=1/s(Yo,m)2 where s(Yo,m) is the error in Yo,m, and I“o”,k and Ic,k the “observed” and calculated intensities of the kth reflection.
6 Peak Generation and "peak_type"
A number of analytical profile shapes can be convoluted with predefined or User defined functions. Analytical convolutions are used where possible.
Convolution implies integration. A function analytically integrated is exact whereas numerical integration is an approximation with an accuracy dependent on the step size used for integration. Accurate numerical convolution is used when analytical convolution is not possible; this makes it possible to include complex functions in the generation of peak shapes.
Numerical convolution is important in regards to laboratory powder diffraction data as many of the instrument aberration functions cannot be convoluted analytically. The process of convolution from a fundamental parameters perspective is an approximation whereby second order effects and higher are typically neglected. These approximations are valid except for extreme cases that are unlikely to exist in practice, for example, axial divergence with Soller slits acceptance angles that are greater than about 12 degrees.
6.1 Source emission profiles
Generation of the emission profile is the first step in peak generation. It comprises EM lines, EMk, each of which is a Voigt comprising the parameters la, lo, lh and lg. The reserved parameter name Lam is assigned the lo value of the EMk line with the largest lavalue, this EMk will be called EMREF. It is used to calculate d-spacings. The interpretation of EM data is dependent on peak_type. For all peak types the position 2qk calculated for a particular emission line for a particular Bragg position of 2q is determined as follows:
![]() 2q for xo_Is phases corresponds to the xo parameter. 2q for d_Is phases is given by the Bragg equation 2q=ArcSin(Lam/(2 d)) 360/Pi where d corresponds to the value of the d parameter. 2q values for str and hkl_Is phases are calculated from the lattice parameters.
2q for xo_Is phases corresponds to the xo parameter. 2q for d_Is phases is given by the Bragg equation 2q=ArcSin(Lam/(2 d)) 360/Pi where d corresponds to the value of the d parameter. 2q values for str and hkl_Is phases are calculated from the lattice parameters.
The FWHWk in °2q for an EMk line is determined from the relations provided in Table 6‑1.
When the keyword no_th_dependence is defined then the calculation of 2qk is determined from
2qk = 2q + EM(lo, i)
The macro No_Th_Dependence can be used when refining on non-X-ray data or fitting to negative 2q values (see example NEGX.INP).
The x-axis extent (x1, x2) to which an EM line is calculated is determined by:
![]() where EMREF corresponds to the emission profile with the largest la value. The default for ymin_on_ymax is 0.001. Emission profile data have been taken from Hölzer et al. (1997) and are stored in *.LAM files in the LAM directory.
where EMREF corresponds to the emission profile with the largest la value. The default for ymin_on_ymax is 0.001. Emission profile data have been taken from Hölzer et al. (1997) and are stored in *.LAM files in the LAM directory.
| Table 6‑1 FWHWk in °2q for an EMk line for the different peak types. | |
| FP peak type | |
| PV peak type | |
| SPVII peak type | |
| SPV peak type | |
6.2 Peak generation and peak types
Phase peaks P are generated as follows:
| P = Get(scale) Get(all_scale_pks) I EM(peak_type) Ä Convolutions | (6‑1) |
where the emission profile (EM) is first generated with emission profile lines of type peak_type; the symbol Ä denotes convolution. Peaks are then convoluted with any defined convolutions, multiplied by the scale parameter, multiplied by any defined scale_pks, and then multiplied by an intensity parameter. For xo_Is, d_Is and hkl_Is phases the intensity is given by the I parameter. For str phases it corresponds to the square of the structure factor F2(hkl). Convolutions are normalized and do not change the area under a peak except for the capillary_diameter_mm and lpsd_th2_angular_range_degrees convolutions. The area under the emission profile is determined by the sum of the la parameters; typically they add up to 1.
The definitions of the pseudo-Voigt and PearsonVII functions are provided in Table 6‑2 (symmetric functions) and Table 6‑3 (split functions). The following terms are used:
Symmetric functions
x (2q-2qk) where 2qk is the position of the kth reflection
fwhm full width at half maximum
h PV mixing parameter
Asymmetric functions
fwhm1, fwhm2 fwhm for the left and right composite function
m1, m2 Exponents for the composite functions
h1, h2 PV mixing parameters for the composite functions
Table 6‑2 Unit area peak types for symmetric functions.
| Profile Function | Definition |
| Gaussian, GUA(x) | 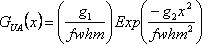 where where |
| Lorentzian, LUA(x) | 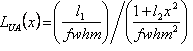 where where |
| PseudoVoigt, PVUA(x) | |
Table 6‑3 Unit area peak types for split functions.
Lorentzian and Gaussian convolutions using lor_fwhm and gauss_fwhm equations are analytically convoluted with FP and PV peak types and numerically convoluted with the SPVII and SPV peak types. These numerical convolutions have a high degree of accuracy as they comprise analytical Lorentzian and Gaussian functions convoluted with straight line segments.
For FP and PV peak types, the first defined hat convolution is analytically convoluted. Additional hat convolutions for all peak types are convoluted numerically.
For classic analytical full pattern fitting the macros PV_Peak_Type, PVII_Peak_Type, TCHZ_Peak_Type can be used. These macros use the following relationships to describe profile width as a function of 2q:
| PV_Peak_Type fwhm = ha + hb tanq + hc/cosq h = lora + lorb tanq + lorc/cosq where ha, hb, hc, lora, lorb, lorc are refineable parameters | PVII_Peak_Type fwhm1 = fwhm2 = ha + hb tanq + hc/cosq m1 = m2 = 0.6 + ma + mb tanq + mc/cosq where ha, hb, hc, ma, mb, mc are refineable parameters |
| TCHZ_Peak_Type: The modified Thompson-Cox-Hastings pseudo-Voigt “TCHZ” is defined as (e.g. Young, 1993), see example ALVO4_TCH.INP, h = 1.36603 q - 0.47719 q2 + 0.1116 q3 where q = GL / G G = (GG5 + AGG4GL + BGG3GL2 + CGG2GL3 + DGGGL4 + GL5)0.2 = fwhm A = 2.69269, B = 2.42843, C = 4.47163, D = 0.07842 GG = (U tan2q + V tanq + W + Z / cos2q)0.5 GL = X tanq +Y / cosq with U, V, W, X, Y, Z as refineable parameters. | |
6.3 Convolution and the peak generation stack
The emission profile of a peak P0 of a certain peak type (ie. FP, PV etc…) is first calculated and placed onto a ‘Peak calculation stack’. P0 analytically includes lor_fwhm and gauss_fwhm convolutions for FP and PV peak types and additionally one hat convolution if defined; the hat convolution is included analytically only if its corresponding num_hats has a value of 1 and if it does not take part in stack operations. Further defined convolutions are convoluted with the top member of the stack. The last convolution should leave the stack with one entry representing the final peak shape. The following keywords allow for manipulation of the Peak calculation stack:
[push_peak]…
[bring_2nd_peak_to_top]…
[add_pop_1st_2nd_peak]…
[scale_top_peak E]…
push_peak duplicates the top entry of the stack; bring_2nd_peak_to_top brings the second most recent entry to the top of the stack and add_pop_1st_2nd_peak adds the top entry to the second most recent entry and then pops the stack. scale_top_peak scales the peak at the top of the stack. As an example use of these keywords consider the generation of back-to-back exponentials as required by GSAS time of flight peak shape 3:
push_peak
prm a0 481.71904 del = 0.05 Val + 2;
prm a1 -241.87060 del = 0.05 Val + 2;
exp_conv_const = a0 + a1 / D_spacing;
bring_2nd_peak_to_top
prm b0 -3.62905 del = 0.05 Val + 2;
prm b1 6.44536 del = 0.05 Val + 2;
exp_conv_const = b0 + b1 / D_spacing^4;
add_pop_1st_2nd_peak
The first statement push_peak pushes P0 onto the stack leaving two peaks on the stack, or,
Stack = P0, P0
The top member is then convoluted by the first exp_conv_const convolution, or,
Stack = P0, P0 Ä exp_conv_const
where Ä denotes convolution. bring_2nd_peak_to_top results in the following:
Stack = P0 Ä exp_conv_const, P0
and the next convolution results in:
Stack = P0 Ä exp_conv_const, P0 Ä exp_conv_const
Thus the stack contains two peaks convoluted with exponentials. The last statement add_pop_1st_2nd_peak produces:
Stack = P0 Ä exp_conv_const + P0 Ä exp_conv_cons
6.4 Speed / Accuracy and peak_buffer_step
For computational efficiency phase peaks are calculated at predefined 2qintervals in a “peaks buffer“. In between peaks are determined by stretching and interpolating. Use of the peaks buffer dramatically reduces the number of peaks actually calculated. Typically no more than 50 to 100 peaks are necessary in order to accurately describe peaks across a whole diffraction pattern. The following keywords affect the accuracy of phase peaks:
[peak_buffer_step !E]
[convolution_step #]
[ymin_on_ymax #]
[aberration_range_change_allowed !E]
Default values for these are typically adequate. peak_buffer_step determines the maximum x-axis spacing between peaks in the peaks buffer, it has a default value of 500*Peak_Calculation_Step. A value of zero will force the calculation of a new peak in the peaks buffer for each peak of the phase. Note that peaks are not calculated for x-axis regions that are void of phase peaks.
convolution_step defines an integer corresponding to the number of calculated data points per measurement data point used to calculate the peaks in the peaks buffer, see x_calculation_step as well. Increasing the value for convolution_step improves accuracy for data with large step sizes or for peaks that have less than 7 data points across the FWHM.
ymin_on_ymax determines the x-axis extents of a peak (see also section 6.1).
aberration_range_change_allowed describes the maximum allowed change in the x-axis extent of a convolution aberration before a new peak is calculated for the peaks buffer. For example, in the case of axial_conv the spacing between peaks in the peaks buffer should be small at low angles and large at high angles. aberration_range_change_allowed is a dependent of the peak type parameters and convolutions as shown in Table 6‑4.
Small values for aberration_range_change_allowed reduces the spacing between peaks in the peaks buffer and subsequently increase the number of peaks in the peaks buffer.
Table 6‑4 Default values for aberration_range_change_allowed for the following peak type parameters and convolutions.
| Parameter | Default aberration_range_change_allowed |
| m1, m2 | 0.05 |
| h1, h2, pv_fwhm, spv_h1, spv_h2 | Peak_Calculation_Step |
| pv_lor, spv_l1, spv_l2 | 0.01 |
| hat, axial_conv, whole_hat, half_hat | Peak_Calculation_Step |
| one_on_x_conv, exp_conv_const, circles_conv | Peak_Calculation_Step |
| lor_fwhm and gauss_fwhm | Peak_Calculation_Step for all lor_fwhm and gauss_fwhm defined. |
7 Miscellanous
7.1 Instrument and sample convolutions
Diffractometer instrument and sample aberration functions used for peak profile synthesis are generated from generic convolutions. For example, the “simple” axial divergence model is described using the generic convolution circles_conv as defined in the Simple_Axial_Model macro. Table 7‑1 lists some of the instrument convolutions supported. In addition the full axial divergence model of Cheary & Coelho (1998a, 1998b) is supported.
Table 7‑1 Instrument and sample aberration functions in terms of ![]() , where 2q is the measured angle and 2qk the Bragg angle. RP and RS correspond to the primary and secondary radius of the diffractometer respectively.
, where 2q is the measured angle and 2qk the Bragg angle. RP and RS correspond to the primary and secondary radius of the diffractometer respectively.
7.2 Microstructure convolutions
The Double-Voigt approach (e.g. Balzar, 1999) is supported for modeling microstructure effects. Crystallite size and strain comprise Lorentzian and Gaussian component convolutions varying in 2q as a function of 1/cos(q) and tan(q) respectively.
7.2.1 Preliminary equations
The following preliminary equations are based on the unit area Gaussian, GUA(x), and Lorentzian, LUA(x), and pseudo-Voigt PVUA(x) functions as given in Table 6‑2.
Height of GUA(x) and LUA(x) respectively
GUAH = GUA(x=0) = g1 / fwhm
LUAH = LUA(x=0) = l1 / fwhm
Gaussian and Lorentzian respectively with area A
G(x) = A GUA(x)
L(x) = A LUA(x)
Height of G(x) and L(x) respectively
GH = A GUA
LH = A LUAH
Integral breadth of Gaussian and Lorentzian respectively
bG = A / GH = 1 / GUAH = fwhm / g1
bL = A / LH = 1 / LUAH = fwhm / l1
Unit area Pseudo Voigt, PVUA
PVUAH = h LUAH + (1-h) GUAH
bPV = 1 / PVUAH
A Voigt is the result of a Gaussian convoluted by a Lorentzian
V = G(fwhmG) Ä L(fwhmL)
where “Ä” denotes convolution and fwhmG and fwhmL are the FWHM of the Gaussian and Lorentzian components.
A Voigt can be approximated using a Pseudo Voigt. This is done numerically where
V(x) = G(fwhmG) Ä L(fwhmL) = PVUA(x, fwhmPV)
By changing units to s (Å-1)
s = 1/d = 2 sin(q) / l
and differentiating and approximating ds/dq = Ds /Dq we get
Ds = (2 cos(q) / l) Dq
thus,
fwhm(s) = fwhm(2q) cos(q) / l
IB(s) = IB(2q) cos(q) / l
7.2.2 Crystallite size and strain
Crystallite Size
For crystallite size the Gaussian and Lorentzian component convolutions are:
fwhm(2q) of Gaussian = (180/p) l / (cos(q) CS_G)
fwhm(2q) of Lorentzian= (180/p) l / (cos(q) CS_L)
b(2q) of Gaussian = (180/p) l / (cos(q) CS_G g1)
b(2q) of Lorentzian = (180/p) l / (cos(q) CS_L l1)
or, according to Balzar (1999), in terms of s, bGS and bCS
fwhm(s) of Gaussian = (180/p) / CS_G
fwhm(s) of Lorentzian = (180/p) / CS_L
bGS(s) =b(s) of Gaussian = (180/p) / (CS_G g1)
bCS(s) =b(s) of Lorentzian = (180/p) / (CS_L l1)
The macros CS_L and CS_G are used for calculating the CS_L and CS_G parameters respectively.
Determination of the volume weighted mean column height LVol, LVol-IB and LVol-FWHM is as follows:
LVol-IB = k / Voigt_Integral_Breadth_GL (1/CS_G, 1/CS_L)
LVol-FWHM = k / Voigt_FWHM(1/CS_G, 1/CS_L)
The macro LVol_FWHM_CS_G_L is used for calculating LVol-IB and LVol-FWHM.
Strain
Strain_G and Strain_L parameters corresponds to the fwhm(2q) of a Gaussian and a Lorentzian that is convoluted into the peak, or,
fwhm(2q) of Gaussian = Strain_G tan(q)
fwhm(2q) of Lorentzian= Strain_L tan(q)
b(2q) of Gaussian = Strain_G tan(q) / g1
b(2q) of Lorentzian = Strain_L tan(q) / l1
or, according to Balzar (1999), in terms of s, bCD and bGD
fwhm(s) of Gaussian = Strain_G sin(q) / l = Strain_G s / 2
fwhm(s) of Lorentzian = Strain_L sin(q) / l = Strain_L s / 2
bGD(s)/s0 s = b(s) of Gaussian = (Strain_G / g1) s / 2
bCD(s)/s0 s = b(s) of Lorentzian = (Strain_L / l1) s / 2
The macros Strain_L and Strain_G are used for calculating the Strain_L and Strain_G parameters respectively.
From these equations we get:
bGD(s) = s0 Strain_G / (2 g1)
bCD(s) = s0 Strain_L / (2 l1)
According to Balzar (1999), equation (34):
e = bD(2q) / (4 tan(q))
where bD(2q) is the fwhm of a Voigt comprising a Gaussian with a fwhm = Strain_G Tan(q) and a Lorentzian with a fwhm = Strain_L Tan(q).
The value for e0 is given by:
4 e0 Tan(q) = FWHM of the Voigt from Strain_L and Strain_G
= Voigt_FWHM(Strain_L, Strain_G) Tan(q)
or,
e0 = Voigt_FWHM(Strain_L, Strain_G) / 4
The macro e0_from_Strain calculates e0 using the equation function Voigt_FWHM_GL.
7.3 Calculation of structure factors
The structure factor F for a particular reflection (h k l) is the complex quantity:
| F = Ss (AS + i BS) Sa (fo,a + fa' + i fa”) Oa | (7‑1) |
The summation Ss is over the sites of the unit cell and the summation Sa is over the atoms residing on site s. Oa and fo,a corresponds to the site occupancy and the atomic scattering factor for atom ’a’ respectively. fa' and fa“ are the anomalous dispersion coefficients for atom ’a’. AS and BS corresponds to the cosine and sine summations for site 's', or:
| AS = Se Ts,e cos(2p h . re), BS = Se Ts,e sin(2p h . re) | (7‑2) |
where Ts,e is the temperature factor and the summation Se is over the equivalent positions of site 's' as dictated by the space group. Defining:
| fo,s = Sa fo,a Oa, fs' = Sa fa' Oa, fs” = Sa fa“ Oa | (7‑3) |
and separating the real and imaginary components gives:
| F = Ss (As + i Bs) (fo,s + fs'+ i fs”) F = Ss (As (fo,s +fs') - Bs fs“) + i Ss (As fs” + Bs (fo,s + fs')) or, F = A + i B | (7‑4) |
The observed intensity is proportional to the complex conjugate of the structure factor, or,
| F2 = A2 + B2 | (7‑5a) |
or,
| F2 = A012 + B012 + A112 + B112 + 2 B01 A11 - 2 A01 B11 | (7‑5b) |
| where A01= Ss As (fo,s + fs'), A11 = Ss As fs“ B01= Ss Bs (fo,s + fs'), B11 = Ss Bs fs” and A = A01 - B11, B = B01 + A11 |
Atomic scattering factors used, fo,a, are by default those from
http://www.esrf.fr/computing/expg/subgroups/theory/DABAX/dabax.html
these comprise 11 values per atom and are found in the file ATMSCAT_11.CPP. Correspondingly 9 values per atom, obtained from the International Tables, are found in the file ATMSCAT_9.CPP. Use of either 9 or 11 values can be invoked by running the batch files use_9f0 and use_11f0 respectivelly.
Dispersion coefficients used, fa' and fa“, are by default from
http://www.cxro.lbl.gov/optical_constants/asf.html
These data, found in the SSF directory, covers the energy range from 10 to 30000eV. The use of use_tube_dispersion_coefficients forces the use of dispersion coefficients from the International Tables for X-ray Crystallography [1995], Vol.C, p384-391 and 500-502, and for O2- from Hovestreydt [1983]. These data are in discrete energy steps corresponding to wavelengths typically found in laboratory X-ray tubes.
For neutron diffraction data fa'= fa”=0 and fo,a is replaced by the bound coherent scattering length (found in the NEUTSCAT.CPP file) for atom ‘a’ obtained from
http://www.ccp14.ac.uk/ccp/web-mirrors/neutrons/n-scatter/n-lengths/LIST~1.HTM
7.3.1 Friedel pairs
For centrosymmetric structures the intensities for a Friedel reflection pair are equivalent, or, F2(h k l) = F2(-h-k-l). This holds true regardless of the presence of anomalous scattering and regardless of the atomic species present in the unit cell. This equivalence in F2 is due to the fact that B01 = B11 = 0 and thus:
| F = A01 + i A11 and F2 = A012 + A112 | (7‑6) |
For non-centrosymmetric structures and for the case of no anomalous scattering, or for the case where the unit cell comprises a single atomic species, then F2(h k l) = F2(-h-k-l). Or, for a single atomic species we have:
| B01 A11 = (f0 +f') (SS BS) f“ (SS AS), A01 B11 = (f0 +f') (SS AS) f” (SS BS) or, B01 A11 = A01 B11 | (7‑7) |
and thus from cancellation in Eq. (7‑5b) we get
| F2(h) = F2(-h) = A012 + B012 + A112 + B112 | (7‑8) |
For non-centrosymmetric structures and for the case of anomalous scattering and for a structure comprising more than one atomic species then F2(h) ¹ F2(-h).
7.3.2 Powder data
Friedel pairs are merged for powder diffraction data meaning that the multiplicities as determined by the hkl generator includes the reflections (h k l) and (-h -k -l); this merging of Friedel pairs improves computational efficiency. Eq. (7‑5b) gives the correct intensity for unmerged Friedel pairs and thus it cannot be used for merged Friedel pairs. Using the fact that:
| A01(h) = A01(-h), A11(h) = A11(-h) B01(h) = B01(-h), B11(h) = B11(-h) | (7‑9) |
then F2 from Eq. (7‑5b) in terms of B01(h) and B11(h) evaluates to:
| F2(h) = Q1 + Q2 F2(-h) = Q1 – Q2 where Q1 = A012 + B012 + A112 + B112 and Q2 = 2 (B01 A11 – A01 B11) | (7‑10) |
and for merged Friedel pairs we get:
| F2(h) + F2(-h) = 2 Q1 | (7‑11) |
The factor 2 in Eq. (7‑11) is dropped due to the fact that the multiplicity as given by the hkl generator includes this factor. Thus the final equation describing F2 for powder diffraction data for merged Friedel pairs is given by:
| F2(h)merged = Q1 | (7‑12) |
The reserved parameter names of A01, A11, B01 and B11 can be used to obtain unmerged real, imaginary and F2 components and the merged F2. The following macros have been provided in TOPAS.INC:
macro F_Real_positive { (A01-B11) }
macro F_Real_negative { (A01+B11) }
macro F_Imaginary_positive { (A11+B01) }
macro F_Imaginary_negative { (A11-B01) }
macro F2_positive { (F_Real_positive^2 + F_Imaginary_positive^2) }
macro F2_negative { (F_Real_negative ^2 + F_Imaginary_negative^2) }
macro F2_Merged { (A01^2 + B01^2 + A11^2 + B11^2) }
Note that F2_Merged = (F2_positive + F2_negative) / 2
The reserved parameters I_no_scale_pks and I_after_scale_pks for str phases are equivalent to the following:
I_no_scale_pks = Get(scale) M F2_Merged
I_after_scale_pks = Get(all_scale_pks) Get(scale) M F2_Merged
In addition the macros Out_F2_Details and Out_A01_A11_B01_B11 can be used to output F2 details.
7.3.3 Single crystal data
SHELX HKL4 single crystal data comprise unmerged equivalent reflections and thus Eq. (7‑5b) is used for calculating F2. Equivalent reflections are merged by default and can be unmerged using the dont_merge_equivalent_reflections keyword. For centrosymmetric structures, merging includes the merging of Friedel pairs and thus Eq. (7‑12) is used for calculating F2. For non-centrosymmetric structures, merging excludes the merging of Friedel pairs and thus (7‑5b) is used for calculating F2. The keyword dont_merge_Friedel_pairs prevents the merging of Friedel pairs. The ignore_differences_in_Friedel_pairs keyword forces the use of Eq. (7‑12) for calculating F2. The reserved parameter name Mobs returns the number of observed reflections belonging to a particular family of reflections.
Merging of equivalent reflections reduces the computational effort and is useful in the initial stages of structure refinement. Only a single intensity is calculated for a set of equivalent reflections even in the absence of merging. Thus equivalent reflections and Friedel pairs are remembered and intensities appropriated as required.
*.SCR data is typically generated from a powder pattern and comprises merged equivalent reflections including merged Friedel pairs. As a consequence Eq. (7‑12) is used for calculating F2; any definitions of dont_merge_equivalent_reflections,dont_merge_Friedel_pairs and ignore_differences_in_Friedel_pairs are ignored.
7.3.4 The Flack parameter
For single crystal data and for non-centrosymmetric structures the Flack parameter (Flack, 1983) as implemented scales F2(h) and F2(-h) as defined in Eq. (7‑13).
| F2(h) = Q1 + (1 – 2 Flack) Q2 F2(-h) = Q1 – (1 – 2 Flack) Q2 | (7‑13) |
See the test example YLIDMA.INP.
7.3.5 Single Crystal Output
The macro Out_Single_Crystal_Details, see below, outputs details for a single crystal refinement, see test example YLIDMA.INP. Mobs corresponds to the number of observed reflections belonging to a particular family of planes. When Friedel Pairs are not merged then there will be a different Mobs for h and –h. Phase symmetry is considered in the values for A01, B01, A11 and B11.
macro Out_Single_Crystal_Details(file)
{
phase_out file load out_record out_fmt out_eqn
{
“%4.0f” = H;
“%4.0f” = K;
“%4.0f” = L;
“%4.0f” = Mobs;
“%4.0f” = M;
“ %11.4f” = A01;
“ %11.4f” = A11;
“ %11.4f” = B01;
“ %11.4f” = B11;
' I_no_scale_pks
' = Get(scale) Mobs (A01-B11)^2 + (B01+A11)^2; when
' ignore_differences_in_Friedel_pairs is NOT defined.
' = Get(scale) Mobs (A01^2 + B01^2 + A11^2 + B11^2); when
' ignore_differences_in_Friedel_pairs IS defined
' If there are no scale_pks then:
' I_no_scale_pks = I_after_scale_pks = Ycalc
“ %11.4f” = I_no_scale_pks;
“ %11.4f” = I_after_scale_pks;
“ %11.4f” = Ycalc;
“ %11.4f” = Yobs;
“ %11.4f\n” = SigmaYobs;
}
}
7.4 Large refinements with tens of 1000s of parameters
Refinements comprising many parameters and data points can be both slow and memory intensive. Computation speed is hindered by the A matrix dot products of Eq. (5‑5) and in the case of dense matrices memory usage in forming the full A matix can be prohibitive. The following keywords can be used to overcome these problems:
conserve_memory
bootstrap_errors 100
A_matrix_memory_allowed_in_Mbytes 100
A_matrix_elements_tollerance 0.00001
The approximate_A keyword avoids the calculation of the A matrix dot products. Typically more refinement iterations are required for convergence but in most large problems the time to convergence is greatly decreased (see for example AE14-APPROX-A.INP). Furthermore memory usage of the A matrix can be limited using A_matrix_memory_allowed_in_Mbytes; this produces a sparse matrix, dependening on alloted memory, by removing small Aij values.
Typically the calculation of the covariance matrix is impractical and hence errors can instead be determined using the bootstrap method.
7.5 Space groups, hkls and symmetry operators
[space_group $symbol] is used to define the space group where $symbol can be any space group symbol occurring in the file SGCOM5.CPP ( case insensitive), it can also be a space group number; here are some examples:
space_group “I a -3”
space_group ia-3
space_group P_63_M_C
space_group I_41/A_M_D
space_group I_41/A_M_D:2 ' defines second setting of I_41/A_M_D
space_group 206
space_group 222:2 ' defines second setting of 222
Symmetry operators are generated by SGCOM6.EXE and placed into a sg\*.sg file with a name similar to the name of the space group. Space group names containing the characters ‘/’ or ‘:’ are placed in files with names similar to the space group but with the characters replaced by ‘o’ and ‘q’ respectively. The reason for this is that file names containing these characters are not allowed on some operating systems. hkl generation uses information in the *.sg file.
7.6 Site identifying strings
Keywords such as operate_on_points use a site identifying string; this string can contain the wild card character ’*’ and a negation character ’!’. The wild card character ‘*’ used in “O*” means that sites with names starting with ‘O’ are considered. In addition to using the wild card character, the site names can be explicitly written within double quotation marks. For example, consider the following segment:
str
site Pb1…
site S1 …
site O1 …
site O2 …
site O31 …
site O32 …
site O4 …
Table 7‑2 shows some operate_on_points strings and the corresponding sites identified for this particular example.
Table 7‑2 Example operate_on_points strings and the corresponding sites identified.
| operate_on_points $sites: | Sites identified |
| * | Pb1, S1, O1, O2, O31, O32, O4 |
| Pb* | Pb1 |
| “Pb1 S*“ | Pb1, S1 |
| O* | O1, O2, O31, O32, O4 |
| “O* !O3*“ | O1, O2, O4 |
| “O* !O1 !O2“ | O31, O32, O4 |
7.7 Occupancies and symmetry operators
Only unique positions are generated from symmetry operators. Fully occupied sites therefore require site occupancy values of 1. A comparison of atomic positions is performed in the generation of the unique positions with a tolerance in fractional coordinates of 10-15. It is therefore necessary to enter fractions in the form of equations when entering fractional atomic coordinates that have recurring values such as 0.33333…, 0.666666… etc., for example, use
x = 1/3; y = 1/3; z = 2/3;
instead of
x 0.33333 y 0.33333 z 0.66666
7.8 Pawley and Le Bail extraction
For Pawley intensity extraction (see example PAWLEY1.INP) the following input segment can be used
hkl_Is
space_group p-1
For Le Bail intensity extraction (see example LEBAIL1.INP) the following input segment can be used
hkl_Is
lebail 1
space_group p-1
hkls are generated if there are no hkl_m_d_th2 and I keywords defined. After refinement, the details for the generated hkl’s are appended after the space_group keyword. For the Pawley method, once the hkl details are generated, parameter equations can be applied to the I parameters as usual.
7.9 Anisotropic refinement models
Keywords that can be a function of H, K, L and M, as shown in Table 3‑3, allow for the refinement of anisotropic models including preferred orientation, and peak broadening. An important consideration when dealing with hkls in equations is whether to work with hkls or whether to work with their multiplicities. The Multiplicities_Sum macro can be used when working with multiplicities, for example:
prm a 0
th2_offset = Multiplicities_Sum( If(Mod(L,2)==0, a Tan(Th), 0) );
L here corresponds to the L's of the multiplicities. Note, the preferred orientation macro PO uses the Multiplicities_Sum macro and Spherical Harmonics uses the hkls in the *.hkl file only.
A completely different viewpoint than to refine on half widths is to consider the distribution of lattice metric parameters within a sample. Each crystallite is regarded as having its own lattice parameters, with a multi-dimensional distribution throughout the powder sample. This can be achieved by adding the same structure several times to the input file.
7.9.1 Second rank tensors
Anisotropic peak broadening using the Cagliotti relation:
A qualitative account for anisotropic broadening in profile analysis has been given by Le Bail & Jouanneaux (1997). A macro applying this model could look like the following:
macro LeBail_Jouanneaux_1997(
uc11,uv11,uc22,uv22,
uc33,uv33,uc23,uv23,
uc13,uv13,uc12,uv12,
vc11,vv11,…)
{
prm u 0 min -1 max 2
prm v 0 min -1 max 1
prm w 0.01 min -1 max 2
prm uc11 uv11 prm uc22 uv22 prm uc33 uv33
…
u = (
H^2 A_star A_star uc11 +
…
v = (
H^2 A_star A_star vc11 +
…
w = …
gauss_fwhm = u Tan(Th)^2 + v Tan(Th) + w;
}
According to Le Bail & Jouanneaux (1997) the following symmetry restrictions have to be considered:
| Cubic : 11=22=33, 12=13=23 Hexagonal Trigonal : 11=22, 13=23 Tetragonal | Orthorhombic Monoclinic : None Triclinic |
An analogous variation may also be applied to peak shapes, so a maximum of 36 refineable parameters is obtained.
As the Cagliotti relation is a poor performer in describing half width dependence on 2q for X-ray data and as the extremely high parameter number will not allow for stable and reliable refinements, the examples outlined in sections 7.9.2 and 7.9.3 should be preferred as a base for describing anisotropic peak broadening.
7.9.2 Spherical harmonics
The spherical_harmonics_hkl keyword can be applied to both peak shapes for anisotropy and intensities for a preferred orientation correction. Preferred orientation can be described using the PO_Spherical_Harmonics(sh, order) macro, where “sh” is the parameter name and “order” the order of the spherical harmonics. The scale_pks keyword is used to correct peak intensities.
macro PO_Spherical_Harmonics(sh, order)
{
spherical_harmonics_hkl sh
sh_order order
scale_pks = sh;
}
Example CLAY.INP uses spherical_harmonics_hkl for describing anisotropic peak broadening using the exp_conv_const convolution as follows:
str…
spherical_harmonics_hkl sh
sh_order 8
exp_conv_const = (sh-1) Tan(Th);
7.9.3 Miscellaneous models using User defined equations
Anisotropic Gaussian convolution broadening as a function of L (see example ceo2hkl.inp):
str…
prm a 0.1 min 0.0001 max 5
prm b 0.1 min 0.0001 max 5
gauss_fwhm = If(L==0, a Tan(Th) + .2, b Tan(Th));
Anisotropic peak shifts as a function of L (th2_offset):
str…
prm at 0.07 min 0.0001 max 1
prm bt 0.07 min 0.0001 max 1
th2_offset = If(L==0, at Tan(Th), bt Tan(Th));
Description of anisotropic peak broadening using the March (1932) relation and str_hkl_angle:
str…
str_hkl_angle ang1 1 0 0
prm p1 1 min 0.0001 max 2
prm p2 0.01 min 0.0001 max 0.1
lor_fwhm = p2 Tan(Th) Multiplicities_Sum(((p1^2 Cos(ang1)^2 +
Sin(ang1)^2 / p1)^(-1.5)));
7.10 Rigid bodies and bond length restraints
Rigid bodies comprise points in space defined using either the z_matrix or point_for_site keywords or both simultaneously. All or some of these points can then be operated on using the rotate and translate keywords.
Rigid body operations typically comprise:
- Translating a rigid body or part of a rigid body.
- Rotating a rigid body or part of a rigid body around a point.
- Rotating a rigid body or part of a rigid body around a line.
ua, ub, and uc of the point_for_site keyword, ta, tb and tc of the translate keyword, qa, qb and qc of the rotate keyword and the parameters of the z_matrix keyword are all refineable parameters. This means that parameter attributes such as min/max can be defined.
The following Web addresses further describes the use of Z-matrices:
The directory RIGID contains rigid body examples in *.RGD files. These files can be viewed and modified using the Rigid-Body-Editor of the GUI.
7.10.1 Fractional, Cartesian and Z-matrix coordinates
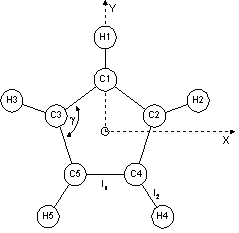
The most basic means of setting up a rigid body is by means of fractional or Cartesian coordinates. A Benzene ring for example without Hydrogens can be formulated as follows:
prm a 1.3 min 1.2 max 1.4
point_for_site C1 ux = a Sqrt(3) .5; uy = a .5;
point_for_site C2 ux = a Sqrt(3) .5; uy = -a .5;
point_for_site C3 ux = -a Sqrt(3) .5; uy = a .5;
point_for_site C4 ux = -a Sqrt(3) .5; uy = -a .5;
point_for_site C5 uy = a;
point_for_site C6 uy = -a;
‘ rotate all previously defined points:
Rotate_about_axies(@ 0, @ 0, @ 0)
‘ translate all previously defined points:
Translate(@ .1, @ .2, @ .3)
The last two statements rotates and translates the rigid body as a whole and their inclusion are implied if absent in the following examples.
A formulation of any complexity can be obtained from a) databases of existing structures and simply using fractional or Cartesian coordinates of structure fragments or b) from sketch programs for drawing chemical structures.
A Z-matrix representation of a rigid body explicitly defines the rigid body in terms of bond lengths and angles. A Benzene ring is typically formulated using two dummy atoms X1 and X2 as follows:
str…
site X1… occ C 0
site X2… occ C 0
rigid
load z_matrix {
X1
X2 X1 1.0
C1 X2 1.3 X1 90
C2 X2 1.3 X1 90 C1 60.0
C3 X2 1.3 X1 90 C2 60.0
C4 X2 1.3 X1 90 C3 60.0
C5 X2 1.3 X1 90 C4 60.0
C6 X2 1.3 X1 90 C5 60.0
}
Atoms with occupancies fixed to zero (dummy atoms) do not take part in structure factor calculations. Importantly however dummy atoms can take part in penalties. The mixing of point_for_site and z_matrix keywords is possible as follows:
rigid
point_for_site X1
load z_matrix {
X2 X1 1.0
C1 X2 1.3 X1 90
…
}
Z-matrix parameters are like any other parameter; they can be equations and parameter attributes can be assigned. For example, the 1.3 bond distance can be refined as follows:
rigid
point_for_site X1
load z_matrix {
X2 X1 1.0
C1 X2 c1c2 1.3 min 1.2 max 1.4 X1 90
C2 X2 =c1c2; X1 90 C1 60.0
C3 X2 =c1c2; X1 90 C2 60.0
C4 X2 =c1c2; X1 90 C3 60.0
C5 X2 =c1c2; X1 90 C4 60.0
C6 X2 =c1c2; X1 90 C5 60.0
}
This ability to constrain Z-matrix parameters through the use of equations allows for great flexibility. Example use of such equations could involve writing a particular Z-matrix bond length parameter in terms of other bond length parameters whereby the average bond length is maintained. Or, in cases where a bond length is expected to change as a function of a site occupancy then an equation relating the bond length as a function of the site occupancy parameter can be formulated.
7.10.2 Translating part of a rigid body
Once a starting rigid body model is defined, further translate and rotate statements can be included to represent deviations from the starting model. For example, if the C1 and C2 atoms are expected to shift by up to 0.1Å and as a unit then the following could be used:
rigid
load z_matrix {
X1
X2 X1 1.0
C1 X2 1.3 X1 90
C2 X2 1.3 X1 90 C1 60.0
C3 X2 1.3 X1 90 C2 60.0
C4 X2 1.3 X1 90 C3 60.0
C5 X2 1.3 X1 90 C4 60.0
C6 X2 1.3 X1 90 C5 60.0
}
translate
tx @ 0 min -.1 max .1
ty @ 0 min -.1 max .1
tz @ 0 min -.1 max .1
operate_on_points “C1 C2”
where the additional statements are outlined in bold. The Cartesian coordinate representation allows an additional means of shifting the C1 and C2 atoms by refining on the ux, uy and uz coordinates directly, or,
prm a 1.3 min 1.2 max 1.4
prm t1 0 min -.1 max .1
prm t2 0 min -.1 max .1
prm t3 0 min -.1 max .1
rigid
point_for_site C1 ux = a Sqrt(3) .5 + t1; uy = a .5 + t2; uz = t3;
point_for_site C2 ux = a Sqrt(3) .5 + t1; uy = -a .5 + t2; uz = t3;
point_for_site C3 ux = -a Sqrt(3) .5; uy = a .5;
point_for_site C4 ux = -a Sqrt(3) .5; uy = -a .5;
point_for_site C5 uy = a;
point_for_site C6 uy = -a;
7.10.3 Rotating part of a rigid body around a point
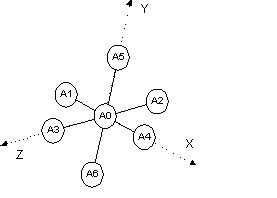
Many situations require the rotation of part of a rigid body around a point. An octahedra (Fig. 7‑1) for example typically rotates around the central atom with three degrees of freedom. To implement such a rotation when the central atom is arbitrarily placed requires setting the origin at the central atom before rotation and then resetting the origin after rotation. This is achieved using the Translate_point_amount macro as follows:
prm r 2 min 1.8 max 2.2
rigid
point_for_site A0
point_for_site A1 ux = r;
point_for_site A2 ux = -r;
point_for_site A3 uy = r;
point_for_site A4 uy = -r;
point_for_site A5 uz = r;
point_for_site A6 uz = -r;
Translate_point_amount(A0, -) operate_on_points “A* !A0”
rotate @ 0 qa 1 operate_on_points “A* !A0”
rotate @ 0 qb 1 operate_on_points “A* !A0”
rotate @ 0 qc 1 operate_on_points “A* !A0”
Translate_point_amount(A0, +) operate_on_points “A* !A0”
The point_for_site keywords could just as well be z_matrix keywords with the appropriate Z-matrix parameters. The first Translate_point_amount statement translates the specified points (A1 to A6) by an amount equivalent to the negative position of A0. This effectively sets the origin for these points to A0. The second Translate_point_amount resets the origin back to A0. If the A0 atom happens to be at Cartesian (0, 0, 0) then there would be no need for the Translate_point_amount statements.
Further distortions are possible by refining on different bond-lengths between the central atom and selected outer atoms. For example, the following macro describes an orthorhombic bipyramid:
macro Orthorhombic_Bipyramide(s0, s1, s2, s3, s4, s5, s6, r1, r2)
{
point_for_site s0
point_for_site s1 ux r1
point_for_site s2 ux –r1
point_for_site s3 uy r1
point_for_site s4 uy –r1
point_for_site s5 uz r2
point_for_site s6 uz –r2
}
Note the two different lengths r1 and r2; with r1 = r2 this macro would describe a regular octahedron.
7.10.4 Rotating part of a rigid body around a line
Rigid bodies can be created by using the rotate and translate keywords instead of explicitly entering fractional or Cartesian coordinates. For example, two connected Benzene rings, a schematic without Hydrogens is shown in Fig. 7‑2, can be formulated as follows:
prm r 1.3 min 1.2 max 1.4
rigid
point_for_site C1 ux = r;
load point_for_site ux rotate qz operate_on_points {
C2 =r; 60 1 C2
C3 =r; 120 1 C3
C4 =r; 180 1 C4
C5 =r; 240 1 C5
C6 =r; 300 1 C6
}
point_for_site C7 ux = r;
load point_for_site ux rotate qz operate_on_points {
C8 =r; 60 1 C8
C9 =r; 120 1 C9
C10 =r; 300 1 C10
}
translate tx = 1.5 r; ty = r Sin(60 Deg);
operate_on_points “C7 C8 C9 C10”
The points of the second ring can be rotated around the line connecting C1 to C2 with the following:
Rotate_about_points(@ 50 min -60 max 60, C1, C2, “C7 C8 C9 C10”)
The min/max statements limit the rotations to ±30 degrees.
C5 can be rotated around the line connecting C4 and C6 with the following:
Rotate_about_points(@ 40 min -50 max 50, C4, C6, C5)
Similar Rotate_about_points statements for each atom would allow for distortions of the Benzene rings without changing bond distances.
7.10.5 Benefits of using Z-matrix together with rotate and translate
Cyclopentadienyl (C5H5)- is a well defined molecular fragment which shows slight deviation from a perfect five-fold ring (Fig. 7‑3). The rigid body definition using point_for_site keywords is as follows:
prm r1 1.19
prm r2 2.24
rigid
load point_for_site ux { C1 =r1; C2 =r1; C3 =r1; C4 =r1; C5 =r1; }
load point_for_site ux { H1 =r2; H2 =r2; H3 =r2; H4 =r2; H5 =r2; }
load rotate qz operate_on_points { 72 1 C2 144 1 C3
216 1 C4 288 1 C5 }
load rotate qz operate_on_points { 72 1 H2 144 1 H3
216 1 H4 288 1 H5 }
and using a typical Z-matrix representation:
rigid
load z_matrix {
X1
X2 X1 1
C1 X2 1.19 X1 90
C2 X2 1.19 X1 90 C1 72
C3 X2 1.19 X1 90 C2 72
C4 X2 1.19 X1 90 C3 72
C5 X2 1.19 X1 90 C4 72
X3 C1 1 X2 90 X1 0
H1 C1 1.05 X3 90 X2 180
H2 C2 1.05 C1 126 X2 180
H3 C3 1.05 C2 126 X2 180
H4 C4 1.05 C3 126 X2 180
H5 C5 1.05 C4 126 X2 180
}
This Z-matrix representation is one that is typically used for Cyclopentadienyl and it allows for various torsion angles. It does not however directly allow for all possibilities, for example, no adjustment of a single parameter allows for displacement of the C1 atom without changing the C1-C2 and C1-C3 bond distances. The desired result however is possible using the Rotate_about_points macro as follows:
Rotate_about_points(@ 0, C2, C3, “C1 H1”)
Thus the ability to include rotate and translate statements together with z_matrix keyword gives greater flexibility in defining rigid bodies.
7.10.6 The simplest of rigid bodies
The simplest rigid body comprises an atom constrained to move within a sphere; for a radius of 1 then this can be can be achieved as follows:
rigid
point_for_site Ca uz @ 0 min -1 max 1
rotate r1 10 qx 1
rotate r2 10 qx = Sin(Deg r1); qy = -Cos(Deg r1);
The coordinates are in fact spherical coordinates; this is preferred as the rotation parameters r1 and r2 are communicative. Constraining an atom to within a sphere is a useful constraint when the approximate atomic position is known.
Setting the distance between two sites, or, two sites A and B a distance 2Å apart can be formulated as:
In Z-matrix form
rigid
z_matrix A ' line 1
z_matrix B A 2 ' line 2
rotate @ 20 qa 1 ' line 3
rotate @ 20 qb 1 ' line 4
translate ta @ .1 tb @ .2 tc @ .3 ' line 5
In Cartesian form
rigid
point_for_site A ' line 1
point_for_site B uz 2 ' line 2
rotate @ 20 qa 1 ' line 3
rotate @ 20 qb 1 ' line 4
translate ta @ .1 tb @ .2 tc @ .3 ' line 5
Lines 1 and 2 defines the two points (note that ux, uy and uz defaults to 0), line 3 and 4 rotates the two points around the a lattice vector and then the b lattice vector respectively and line 5 translates the two points to a position in fractional atomic coordinates of (.1, .2, .3). Lines 3 to 5 contain the five parameters associated with this rigid body.
The Set_Length macro can instead be used to set the distance between the two sites as follows:
Set_Length(A, B, 2, @, @, @, @ 30, @ 30)
where A and B are the site names, 2 is the distance in Å between the sites, arguments 4 to 6 are the names given to the translation parameters and arguments 7 and 8 are the rotational parameters. Set_Length is not supplied with the translate starting values; these are obtained from the A site with the use of the keyword start_values_from_site located in the Set_Length macro .
min/max can be used to constrain the distance between the two sites, for example,
Set_Length(A, B, @ 2 min 1.9 max 2.1, @, @, @, @ 30, @ 30)
Note, this macro defines the distance between the two sites as a parameter that can be refined.
7.10.7 Generation of rigid bodies
A rigid body is constructed by the sequential processing of z_matrix, point_for_site, rotate and translate operations. The body is then converted to fractional atomic coordinates and then symmetry operations of the space group applied.
The conversion of Z-matrix coordinates to Cartesian is as follows:
the first atom, if defined using the z_matrix keyword, is paced at the origin.
the second atom, if defined using the z_matrix keyword, is placed on the positive z-axis.
the third atom, if defined using the z_matrix keyword, is placed in the x-z plane.
The conversion from Cartesian to fractional coordinates in terms of the lattice vectors a, b, anc c is as follows:
x-axis in the same direction as the a lattice vector.
y-axis in the a-b plane.
z-axis in the direction defined by the cross product of a and b.
Rotation operations are not commutative and thus the rotation of a point A about the vector B-C and then about D-E is not the same as the rotation of A about D-E and then about B-C.
By default rotate and translate operate on all previously defined point_for_site’s; alternatively point_for_site’s can be explicitly defined using the operate_on_points keyword which identifies sites (see section 7.6). operate_on_points must refer to previously defined point_for_site’s and it can refer to many sites at once by enclosing the site names in quotes and using the wild card character ‘*’ or the negation character ‘!’, for example:
operate_on_points “Si* O* !O2”
7.11 Simulated annealing and structure determination
Defining continue_after_convergence and a temperature regime is analogous to defining a simulated annealing process. After convergence a new refinement cycle is initiated with parameter values changed according to any defined val_on_continue attributes and rand_xyz or randomize_on_errors processes. Thus simulated annealing is not specific to structure solution, see for example ONLYPENA.INP and ROSENBROCK-10.INP
In regards to structure solution in real space, the need for computation efficiency is critical. In many cases computation speed can be increased by up to a factor of 20 or more with the appropriate choice of keywords. Keywords that facilitate speed are as follows:
quick_refine !E
Another category is one that facilitate structure solution by changing the form of ![]() :
:
penalties_weighting_K1 !E
penalty…
occ_merge…
rigid…
Further keywords and processes typically used are:
file_name_for_best_solutions
seed
swap_sites…
temperature !E…
move_to_the_next_temperature_regardless_of_the_change_in_rwp
save_values_as_best_after_randomization
use_best_values
do_processes
xdd… or xdd_scr…
str…
site … rand_xyz…
break_if_been_there
try_site_patterns…
7.11.1 Penalties used in structure determination
Introducing suitable penalty functions can reduce the number of local minima in ![]() and correspondingly increase the chances of obtaining a global minimum. The structure factor for a reflection with Miller indices 10 0 0 for a two atom triclinic unit cell with fractional atomic coordinates of (0,0,0) and (x, 0,0) is given by 4 cos(phx)2; here there are 10 local minima for 0<x<1. If it was known that the bond length distance is half the distance of the a lattice parameter then a suitable penalty function would reduce the number of minima to one. In this trivial example it can be seen that the number of minima increases as the Miller indices increase. For non-trivial structures and for the important d spacing range near inter-atomic distances of 1 to 2Å the number of local minima is very large. Bragg reflections with large Miller indices that are heavily weighted are expected to contain many false minima; by applying an appropriate weighting scheme to the diffraction data the search for the global minimum can be facilitated. For powder data the default weighting scheme is:
and correspondingly increase the chances of obtaining a global minimum. The structure factor for a reflection with Miller indices 10 0 0 for a two atom triclinic unit cell with fractional atomic coordinates of (0,0,0) and (x, 0,0) is given by 4 cos(phx)2; here there are 10 local minima for 0<x<1. If it was known that the bond length distance is half the distance of the a lattice parameter then a suitable penalty function would reduce the number of minima to one. In this trivial example it can be seen that the number of minima increases as the Miller indices increase. For non-trivial structures and for the important d spacing range near inter-atomic distances of 1 to 2Å the number of local minima is very large. Bragg reflections with large Miller indices that are heavily weighted are expected to contain many false minima; by applying an appropriate weighting scheme to the diffraction data the search for the global minimum can be facilitated. For powder data the default weighting scheme is:
weighting = If(Yobs ⇐ 1, 1, 1 / Yobs);
For single crystal data the following, which is proportional to 1/d, works well:
weighting = 1 / (Sin(X Deg / 2) Max(Yobs,1));
A more elaborate scheme which also works well for single crystal data is as follows:
weighting = ( Abs(Yobs-Ycalc) / Abs(Yobs+Ycalc) +1) / Sin(X Deg / 2);
Two penalty functions that have shown to facilitate the determination of structures are the anti-bumping (AB) penalty and the potential energy penalty U. The anti-bumping penalty is written as:
where r0 is a bond length distance, rij the distance between atoms i and j including symmetry equivalent positions and the summation is over all atoms of type j. The ai_anti_bump and box_interaction keywords are used to implement the penalty of Eq. 7‑15 using the AI_Anti_Bump and Anti_Bump macros respectively.
Typically Anti bump constraints are applied to heavy atoms; an over use of such constraints can in fact hinder simulated annealing in finding the global minimum. Applying the constraint for the first few iterations of a refinement cycle only can also be beneficial; this is achieved in the AI_Anti_Bump macro by writing the penalty in terms of the reserved parameter Cycle_Iter; see for example CIME-DECOMPOSE.INP.
The grs_interaction can be used to either calculate the Lennard-Jones or Born-Mayer potentials and it is suited to ionic atomic models (see example ALVO4-GRS-AUTO.INP). For a particular site i they comprise a Coulomb term Ci and a repulsive term Ri and is written as:
where A = e2/(4pe0) and e0 is the permittivity of free space, Qi and Qj are the ionic valences of atoms i and j, rij is the distance between atoms i and j and the summation is over all atoms to infinity. The repulsive constants Bij, n, cij and d are characteristic of the atomic species and their potential surrounds. The equation part of the grs_interaction is typically used to describe the repulsive terms.
7.11.2 Definition of bond length restraints
The following example defines a bondlength restraint using the GRS series (see example ALVO4-GRS-AUTO.INP) between an Aluminum site and three Oxygen sites. Valence charges have been set to +3 and –2 for Aluminum and Oxygen, respectively. The expected bond length is 2 Angstroms between Oxygen sites and 1.5 Angstroms between Aluminum and Oxygen sites.
site Al x @ 0.7491 y @ 0.6981 z @ 0.4069 occ Al+3 1 beq 0.25
site O1 x @ 0.6350 y @ 0.4873 z @ 0.2544 occ O-2 1 beq 1
site O2 x @ 0.2574 y @ 0.4325 z @ 0.4313 occ O-2 1 beq 1
site O3 x @ 0.0450 y @ 0.6935 z @ 0.4271 occ O-2 1 beq 1
Grs_Interaction(O*, O*, -2, -2, oo, 2.0, 5) penalty = oo;
Grs_Interaction(Al, O*, 4, -2, alo, 1.5, 5) penalty = alo;
The following example defines a bondlength restraint using the AI_Anti_Bump macro between a Potassium site and three Carbon sites. The expected bond length is 4 Angstroms between Potassium sites and 1.3 Angstroms between Carbon sites.
site K x @ 0.14305 y @ 0.21812 z @ 0.12167 occ K 1 beq 1
site C1 x @ 0.19191 y @ 0.40979 z @ 0.34583 occ C 1 beq 1
site C2 x @ 0.31926 y @ 0.35428 z @ 0.32606 occ C 1 beq 1
site C3 x @ 0.10935 y @ 0.30991 z @ 0.39733 occ C 1 beq 1
AI_Anti_Bump(K , K , 4 , 1)
AI_Anti_Bump(C*, C*, 1.3, 1)
Note, there's no explicit definition of a penalty function as in the first example. The AI_Anti_Bump macro already includes a predefined penalty function.